中文字幕第五页-中文字幕第页-中文字幕韩国-中文字幕最新-国产尤物二区三区在线观看-国产尤物福利视频一区二区

搜索二叉樹

    二叉查找樹（Binary Search Tree）,也稱有序二叉樹（ordered binary tree）,排序二叉樹（sorted binary tree），是指一顆空樹或者具有下列性質的二叉樹：

創(chuàng)新互聯(lián)專注于桑日網站建設服務及定制，我們擁有豐富的企業(yè)做網站經驗。 熱誠為您提供桑日營銷型網站建設，桑日網站制作、桑日網頁設計、桑日網站官網定制、微信小程序定制開發(fā)服務，打造桑日網絡公司原創(chuàng)品牌,更為您提供桑日網站排名全網營銷落地服務。

    （1）每個節(jié)點都有一個作為搜索依據的關鍵碼（key），所有的節(jié)點的關鍵碼互不相同。

    （2）左子樹上所有的關鍵碼（key）都小于根節(jié)點點的關鍵碼（key）。

    （3）右子樹上所有的關鍵碼（key）都大于根節(jié)點的關鍵碼（key）。

    （4）左右子樹都是二叉搜索樹。

代碼實現(xiàn)如下：

#include<iostream>
using namespace std;

template<class K,class V>
struct BSTreeNode{
	BSTreeNode<K, V>* _left;
	BSTreeNode<K, V>* _right;
	K _key;
	V _value;
	BSTreeNode(const K& key,const V& value)
		:_key(key)
		, _value(value)
		, _left(NULL)
		, _right(NULL)
	{}
};
template<class K,class V>
class BSTree{
	typedef BSTreeNode<K, V> Node;
public:
	BSTree()
		:_root(NULL)
	{}
	//非遞歸
	bool Insert(const K& key, const V& value)
	{
		if (_root == NULL)
		{
			_root = new Node(key,value);
			return true;
		}
		Node* parent = _root;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		if (parent->_key>key)
		{
			parent->_left = new Node(key,value);
		}
		else
		{
			parent->_right = new Node(key, value);
		}
		return true;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	Node* Find(const K& key)
	{
		if (_root == NULL)
		{
			return NULL;
		}
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return NULL;
	}

	bool Remove(const K& key)
	{
		if (_root == NULL)
		{
			return false;
		}
		Node* parent = NULL;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
				break;
		}
		if (cur == NULL)
			return false;

		Node* del;
		//刪除節(jié)點的左為空
		if (cur->_left == NULL)
		{
			del = cur;
			if (parent == NULL)
			{
				_root = cur->_right;
			}
			else
			{
				if (parent->_left == cur)
				{
					parent->_left = cur->_right;
				}
				else
				{
					parent->_right = cur->_right;
				}
			}
			delete del;
		}
		//刪除節(jié)點的右為空
		else if (cur->_right == NULL)
		{
			del = cur;
			if (parent == NULL)
			{
				_root = cur->_left;
			}
			else
			{
				if (parent->_left == cur)
				{
					parent->_left = cur->_left;
				}
				else
				{
					parent->_right = cur->_left;
				}
			}
			delete del;
		}
		//刪除節(jié)點的左右都不為空
		else
		{	//找右樹的最左節(jié)點，也就是右邊最小的數
			parent = cur;
			Node* left = cur->_right;
			while (left->_left)
			{
				parent = left;
				left = left->_left;
			}
			del = left;

			cur->_key = left->_key;
			cur->_value = left->_value;

			if (parent->_left == left)
			{
				parent->_left = left->_right;
			}
			else
			{
				parent->_right = left->_right;
			}
			delete del;
		}
		return true;
	}

	//遞歸
	Node* FindR(const K& key)
	{
		return _FindR(_root,key);
	}
	bool InsertR(const K& key, const V& value)
	{
		return _InsertR(_root,key,value);
	}
	bool RemoveR(const K& key)
	{
		return _RemoveR(_root,key);
	}
protected:
	void _InOrder(Node* root)
	{
		if (root != NULL)
		{
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
	}
	Node* _FindR(Node* root,const K& key)
	{
		if (root == NULL)
		{
			return NULL;
		}
		if (root->_key == key)
		{
			return root;
		}
		if (root->_key > key)
		{
			return _FindR(root->_left,key);
		}
		else
		{
			return _FindR(root->_right,key);
		}
		return NULL;
	}
	bool _InsertR(Node*& root, const K& key, const V& value)
	{
		if (root == NULL)
		{
			root = new Node(key,value);
			return true;
		}
		if (root->_key > key)
		{
			return _InsertR(root->_left,key,value);
		}
		else
		{
			return _InsertR(root->_right,key,value);
		}
		return false;
	}
	bool _RemoveR(Node*& root, const K& key)
	{
		if (root == NULL)
		{
			return false;
		}
		if (root->_key > key)
		{
			return _RemoveR(root->_left,key);
		}
		else if (root->_key < key)
		{
			return _RemoveR(root->_right,key);
		}
		else
		{
			//刪除的節(jié)點的左為空
			if (root->_left == NULL)
			{
				root = root->_right;
			}
			//刪除節(jié)點的右為空
			else if (root->_right == NULL)
			{
				root = root->_left;
			}
			else
			{		//找右邊最左的節(jié)點（即右邊最小的節(jié)點）替換刪除的該節(jié)點（下面程序采用的）。
					//或者找左邊最右的節(jié)點（即左邊最大的節(jié)點）替換刪除的該節(jié)點
				Node* parent = root;
				Node* left = root->_right;
				while (left->_left)
				{
					parent = left;
					left = left->_left;
				}
				root->_key = left->_key;
				root->_value = left->_value;
				if (parent->_left == left)
				{
					parent->_left = left->_right;
				}
				else
				{
					parent->_right = left->_right;
				}
			}
			return true;
		}
		return false;
	}
protected:
	Node* _root;
};


#include "BSTree.h"

void Test1()
{
	int arr[10] = { 0, 1, 3, 5, 4, 2, 7, 8, 6, 9};
	BSTree<int, int> bst;
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i)
	{
		bst.Insert(arr[i],i);
	}
	bst.InOrder();
	BSTreeNode<int, int>* ret1=bst.Find(8);
	if (ret1)
	{
		cout << ret1->_key << ":" << ret1->_value << endl;
	}
	else
		cout << "沒有找到ret1" << endl;

	BSTreeNode<int, int>* ret2=bst.Find(22);
	if (ret2)
	{
		cout << ret2->_key << ":" << ret2->_value << endl;
	}
	else
		cout << "沒有找到ret2" << endl;

	bst.Remove(9);
	bst.Remove(7);
	bst.Remove(8);
	bst.InOrder();

	bst.Remove(0);
	bst.Remove(1);
	bst.Remove(2);
	bst.Remove(3);
	bst.Remove(4);
	bst.Remove(5);
	bst.Remove(6);
	bst.Remove(7);
	bst.Remove(8);
	bst.Remove(9);
	bst.InOrder();

}
void Test2()
{
	int arr[10] = { 0, 1, 3, 5, 4, 2, 7, 8, 6, 9 };
	BSTree<int, int> bst;
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i)
	{
		bst.InsertR(arr[i], i);
	}
	bst.InOrder();

	BSTreeNode<int, int>* ret1 = bst.Find(7);
	if (ret1)
	{
		cout << ret1->_key << ":" << ret1->_value << endl;
	}
	else
		cout << "沒有找到ret1" << endl;

	BSTreeNode<int, int>* ret2 = bst.Find(12);
	if (ret2)
	{
		cout << ret2->_key << ":" << ret2->_value << endl;
	}
	else
		cout << "沒有找到ret2" << endl;
	
	bst.RemoveR(8);
	bst.RemoveR(7);
	cout<<bst.RemoveR(9)<<endl;
	bst.InOrder();

	bst.RemoveR(0);
	bst.RemoveR(1);
	cout << bst.RemoveR(2) << endl;
	bst.RemoveR(3);
	bst.RemoveR(4);
	bst.RemoveR(5);
	bst.RemoveR(6);
	bst.RemoveR(7);
	cout << bst.RemoveR(8) << endl;
	bst.RemoveR(9);
	bst.InOrder();

}
int main()
{
	Test1();
	Test2();
	return 0;
}

運行結果：

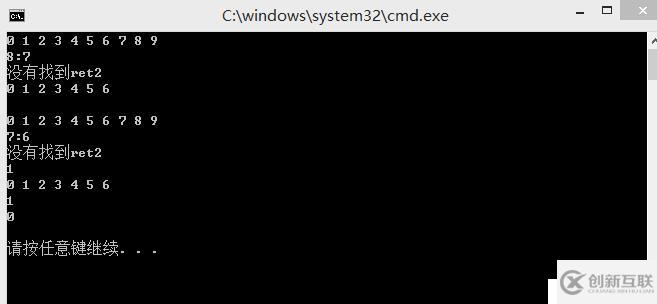
搜索二叉樹

分享名稱：搜索二叉樹
URL鏈接：http://www.2m8n56k.cn/article6/gpocig.html

成都網站建設公司_創(chuàng)新互聯(lián)，為您提供外貿網站建設、軟件開發(fā)、搜索引擎優(yōu)化、品牌網站制作、自適應網站、定制網站

廣告

聲明：本網站發(fā)布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：[email protected]。內容未經允許不得轉載，或轉載時需注明來源： 創(chuàng)新互聯(lián)

外貿網站建設
主站蜘蛛池模板： 国产在线视频一区二区三区 | 男女做性免费视频软件 | 亚洲最大福利视频 | 日韩a一级欧美一级在线播放 | 久久久一区二区三区 | 中国一级大黄大片 | 尹人成人 | 欧美日韩一区二区在线 | 国产欧美日韩在线观看精品 | a级片在线免费观看 | 黄色三级毛片 | 午夜欧美日韩在线视频播放 | 国产精品成人免费综合 | 久草资源在线播放 | 天堂视频网站 | av在线手机播放 | 国产欧美日韩精品在线 | 深夜一级毛片 | 久久99精品九九九久久婷婷 | 国产在线视频欧美亚综合 | 国产精品正在播放 | 成 人 黄 色 免费播放 | 国产高清在线精品二区一 | 日韩精品在线一区 | 香蕉国产人午夜视频在线 | 欧美人成一本免费观看视频 | 欧美一级特黄aa大片 | 好看的看黄a大片爽爽影院 好男人天堂网 | 欧美精品一级 | 韩国一级免费视频 | 亚洲精品永久一区 | 免费国产高清精品一区在线 | 看欧美毛片一级毛片 | 最新亚洲精品国自产在线观看 | 成人影院免费观看 | a级片一级片 | 黄色w站| 亚洲男人天堂2017 | 在线观看欧美一区 | 鲁大师成人精品视频 | 欧美成人久久久免费播放 |